频率学派和贝叶斯学派

一台可以探测太阳是否爆炸且很少说谎的机器报告太阳已经爆炸。 频率学派：“我认为太阳爆炸了。” 贝叶斯学派：“赌你50它没炸。” ——xkcd

统计学有两大学派，分别为频率学派和贝叶斯学派。两者不是仅仅在方法上存在区别，而是从“信仰”层面上看待世界的眼光就截然不同。 频率学派认为数据是可重复的随机样本，但是统计模型中的参数是确定的。而贝叶斯学派则认为观测到的数据是固定的，模型参数是不确定的，并且参数的不确定性可以根据数据更新。

频率学派和贝叶斯学派的一大共同任务是描述统计模型中未知的参数。不同的信仰自然会导致使用不同的工具。

由于统计学派认为参数是确定的，因此不允许使用概率描述参数。参数即是“未知”的，又是“确定”的，看似矛盾，实际不然。“未知”指参数具体的值还不知道，“确定”指虽然不知道参数确切的值，但是可以肯定是它是固定的（不是随机变量）。例如，在运算之前，$123^{456}$的结果是未知的，但是却是确定的，不存在不确定性，因此诸如“$123^{456}$的结果在$10^{400}$到$10^{500}$之间的可能性为2%”等涉及到概率的说法都不对。同样，所有涉及到“概率”、“可能性”等词的参数描述对频率学派而言都是原则上错误的。

由于不能使用概率，频率学派发明了置信区间作为描述未知参数的工具。对于一个事先由研究者确定的置信度$1-\alpha$，频率学派会计算出一个参数区间$[L,U]$，称为“置信区间”，并声称参数“$\theta$以$1-\alpha$的置信度包含在$[L,U]$中。在实际应用中，$\alpha$通常取5%，有时也会取1%或10%。如前面所说，置信度为95%的置信区间，并不表示参数的真实值有95%的概率是在该区间内。由于参数的确定性，在给出置信区间后，参数在不在置信区间内是已经确定的。置信度反应的是该度量的可靠性。频率学派认为数据是可重复的，根据这次实验求的的置信区间和再做一次实验求的置信区间可能是不一样的，这样一直重复地做实验，每次都会计算出一个置信区间，置信度表示这些置信区间中包含真实参数的区间个数所占的比例。在下图中，红色表示真实参数的值，每条绿线表示一次实验求的置信区间。可以看出，有少数置信区间不包含真实参数，置信度反应的就是剩下的包含真实参数的区间所占的比重。这个过程也可看出频率学派的观点：不变的是参数，变化的是数据以及由数据得到置信区间。

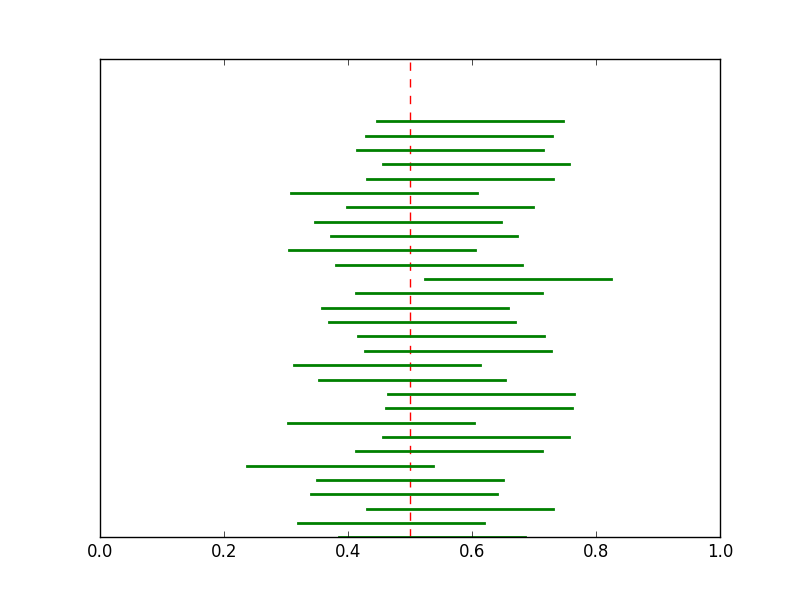
贝叶斯学派则认为参数不仅是未知的，而且是不确定的。为了描述参数的不确定性，贝叶斯学派使用概率作为描述工具。因此，诸如“参数位于某某区间的概率为多少多少”等包含概率的参数描述是贝叶斯学派非常典型的说法。参数在处理上等价于随机变量。 贝叶斯学派解决问题的一般过程是先根据知识和经验为未知的参数$\theta$选择先验概率分布$p(\theta)$， 然后根据观测到的数据使用贝叶斯公式计算得到参数的后验概率

$$\begin{equation} p(\theta\vert X)=\frac{p(\theta)p(X\vert \theta)}{\int p(\theta)p(X\vert \theta) d\theta} \end{equation}$$

由此更新参数的分布。例如，在下图中，蓝色曲线为人选择的参数先验分布，红色为根据数据计算出的参数的后验概率，参数的不确定性得到了更新。

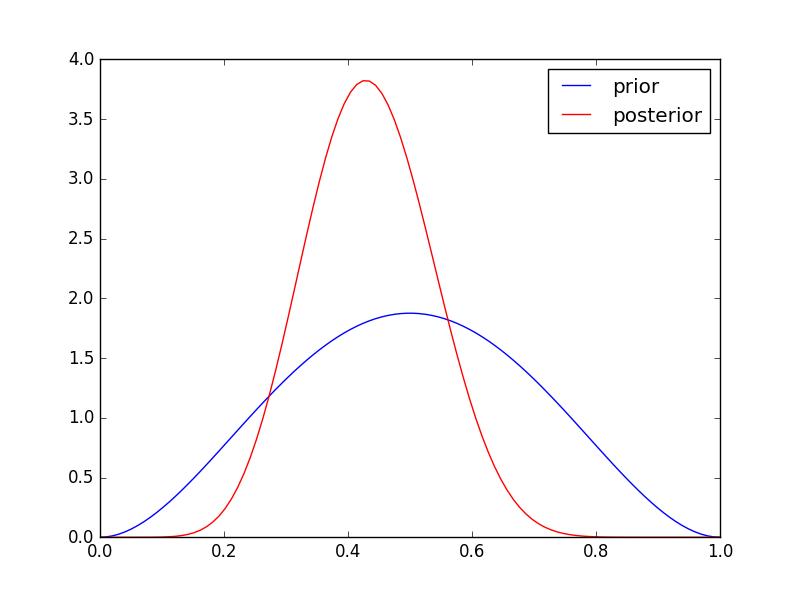
在实际问题中，后验分布的直接求解往往非常困难。比较常见的情况是模型除了可观测随机变量之外，还包含隐含随机变量，使得用贝叶斯公式求参数的后验分布时涉及到对隐含变量的积分，

$$\begin{equation} p(\theta\vert X)=\frac{p(\theta)\int_Zp(X, Z\vert \theta)dZ}{\int p(\theta)\int_Z p(X, Z\vert \theta) dZd\theta} \end{equation}$$

隐含变量维度有可能非常高，进而后验概率无法写出表达式。计算上的困难导致在1950-1990年间，几乎没有人做贝叶斯学派的分析。贝叶斯学派的分析需要大量的计算，而当时计算机不仅非常慢，而且没有普及。频率学派的计算却比较简单，并且模式化，所以在当时受到欢迎。随着计算机科学的发展，以及新的推断方式（马尔科夫链蒙特卡洛、变分）的提出，贝叶斯学派得到了大量的应用，更多实际问题和复杂的模型得以解决。

贝叶斯学派的优点在于， 对于处理含有隐含变量等结构较复杂的模型，贝叶斯学派描述起来更方便。另外，贝叶斯学派能够将已有的知识和经验融入到模型中，从而得到更好的结果。

对于贝叶斯学派，参数先验概率分布的选择非常重要。贝叶斯学派比较受诟病的一点是，其模型参数先验的选取形式在很大程度上是为了计算上的方便，如最常用的一种先验是共轭先验分布。先验选取可以根据研究者的直觉、领域专家的知识经验以及相关的其他方法和数据，很多情况下带有选取者的主观意见。这种主观性经常受到调侃：

问：如果那个笑话里的人不是中国人，而是日本人，那么这个笑话的好笑程度是增加、不变、还是减少？
频率学派的学者：减少。 贝叶斯学派的学者：不变。 贝叶斯学派的中国学者：增加。

贝叶斯学派的学者就是心里觉得自己可能会看到马，但是却瞥见了驴，最后强烈认为自己看到的是骡子的人。

实例

抛起一枚硬币（可能不均衡），硬币落下后正面朝上的概率为$\theta$，反面朝上的概率为$1-\theta$, $\theta$为未知参数。 某次实验共抛了$n$次，其中正面朝上$x$次。

频率学派

参数$\theta$是一个确定的量，抛硬币的过程可以反复一直执行。选取$1-\alpha$为置信度，本次实验的结论是，$\theta$的置信区间为$[L, U]$。其中$L,U$是：

$$\begin{equation} \sum_{k=0}^{x-1}C_n^k L^k (1 - L)^{n-k}=\frac{\alpha}{2} \end{equation}$$ $$\begin{equation} \sum_{k=x+1}^{n}C_n^kU^k(1-U)^{n-k}=1-\frac{\alpha}{2} \end{equation}$$

贝叶斯学派

参数$\theta$是不确定的， 假设$\theta$服从参数为$a, b$的Beta分布，其先验概率为：

$$\begin{equation} p(\theta)=\mathrm{Beta}(\theta\vert a, b)=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\theta^{a-1}(1-\theta)^{b-1} \end{equation}$$

其中

$$\begin{equation} \Gamma(t)=\int_0^\infty x^{t-1}e^{-x}dx \end{equation}$$

本次实验的结论是：$\theta$的后验分布为

$$\begin{equation} p(\theta\vert x)=\frac{p(\theta)p(x|\theta)}{\int p(\theta)p(x|\theta) d\theta} = Beta(\theta\vert a + x, b + n - x) \end{equation}$$

总结

学派	核心思想	度量方法
频率学派	数据可重复采样，参数固定不变	置信区间
贝叶斯学派	数据固定，参数不确定并可以不断更新	后验概率