马尔可夫链蒙特卡洛

马尔可夫链和平稳分布

周末，笨小孩的妈妈出门了，只留笨小孩一个人在家做作业。笨小孩想看电视，但是被妈妈回来看见会挨揍。所以，笨小孩每看1分钟电视或做1分钟作业就要随机地决定是继续当前的活动还是换到另外一个活动：如果当时正在看电视，继续看电视的概率为$T_{tt}$，换为做作业的概率为$T_{th}=1-T_{tt}$；如果当时在做作业，继续做作业的概率为$T_{hh}$，换为看电视的概率为$T_{ht}=1-T_{hh}$。笨小孩挨揍的概率是多少？

记笨小孩在第$i$分钟的活动为$X_i$。笨小孩下次活动的概率只与当前的活动有关，只要当前的活动是看电视，不管之前做了多少作业、看了多少电视，下一步做作业的概率都是$T_{th}$，看电视的概率都是$T_{tt}$；只要当前的活动是做作业，不管之前做了多少作业、看了多少电视，下一步做作业的概率都是$T_{hh}$，看电视的概率都是$T_{ht}$。

这种下一个状态$X_{i+1}$只由当前状态$X_{i}$决定而与再之前的状态${X_j \vert j<i}$无关的性质

$$P(X_{i+1}\vert X_0,X_1,\cdots,X_i)=P(X_{i+1}\vert X_i),$$

称为马尔可夫性，满足马尔可夫性的随机序列$X_0, X_1, \cdots, X_n$称为马尔可夫链，产生该序列的随机过程称为马尔可夫过程。状态$X_i$的空间不仅可以是离散的，也可以是连续的。

当状态空间是离散时，状态间转移的概率可以用转移矩阵$T$表示，$T_{ij}$表示由状态$i$转到状态$j$的概率，显然转移矩阵$T$需要满足

$$T_{ij} \ge 0\\ \sum_j T_{ij} = 1.$$

如果状态空间时连续的，无穷不可数个状态之间的转移概率不可能用转移矩阵表示。用来表示状态转移概率的是马尔可夫核$p(x, x’)$，它表示由状态$x$转移到$x’$的概率密度函数，因此必须满足

$$p(x, x') \ge 0\\ \int_x p(x, x') dx = 1.$$

笨小孩是否挨揍取决于他妈妈回来时他是否在看电视。设妈妈在第$n$分钟回来，笨小孩挨揍的概率为也就是在$n$分钟看电视的概率$P(X_n=t)$。为了求$P(X_n=t)$，可以先求$P(X_i), i=1, 2, \cdots, n$。

假如已经知道第$i$分钟笨小孩的活动的概率$P(X_i)$，第$i+1$分钟笨小孩活动的概率则为

$$P(X_{i+1})=\sum_{X_i\in\{t, h\}}P(X_i)P(X_{i+1}\vert X_i).$$

上式是一个递推公式。只要知道最开始笨小孩选择活动的概率$P(X_0)$和各个活动间转换的概率，就可以求出第$n$分钟活动的概率$P(X_n)$。

例如，如果$P_{tt}=0.1, P_{hh}=0.3$，可以计算笨小孩分别以$1.0, 0.5, 0.3, 0.0$为初始看电视概率的情况下在各个时间挨揍的概率，结果如下图所示。

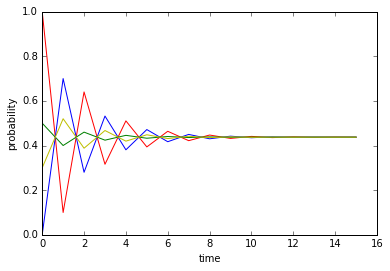
令人感到吃惊的是，不管笨小孩初始看电视的概率为多少，经过一段足够长的时间，笨小孩最后挨揍的概率都一样，并且不再随时间变化，收敛到一种稳定状态。也就是说，最初看电视的概率对后面挨揍概率的影响逐渐减小直至完全消失。

一段时间后不再随时间变化的挨揍概率是否是由活动转换概率决定的呢？再设$P_{tt}=0.2, P_{hh}=0.6$，重新绘制结果：

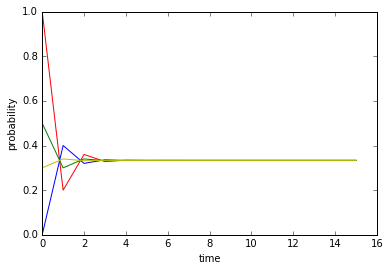
一段时间后，不管初始看电视概率为何，笨小孩挨揍的概率又变得一样，只不过这次与上次稳定时的概率不同。

从这两个结果可以发现一个意外的规律：时间足够长的情况下，计算笨小孩挨揍的概率仅仅需要知道他两个活动间转换的概率，而初始活动的概率P(X_0)甚至确切的时间都可以忽略！

在马尔可夫过程中，这种一段足够长时间后状态所服从的不再随时间变化的概率分布称为平稳分布（stationary distribution），记为

$$\pi(X)=\lim_{n\rightarrow \infty}P(X_n).$$

对于离散状态空间的马尔可夫过程，平稳分布应满足

$$\pi(X＝j)=\sum_i \pi(X＝i)T_{ij}$$

对于连续状态空间的马尔可夫过程，平稳分布应满足

$$\pi(x)=\int_{x'} \pi(x')p(x', x)dx'$$

如果一个马尔可夫过程的平稳分布存在，只要给定状态转移的概率分布，就可以确定出这个唯一的平稳分布。

马尔可夫链蒙特卡洛

笨小孩挨揍了几次之后，希望将以后挨揍的风险控制为$r$。他应该采取什么偷看电视的策略？

笨小孩最先想到的策略是，将时间分为多个周期，每个周期的前$r$部分做作业，后$1-r$部分看电视。如果妈妈回来的时间在每个周期内是均匀分布的，笨小孩就可以将挨揍的风险控制为$r$。但问题是，他不能保证妈妈回来的时间均匀性，当然他也不敢对妈妈说：“妈妈，你能不能在每个半小时内都均匀随机地选择一个时间回来？”

对笨小孩而言，妈妈回来的时间是不可控的，所以上一种方法不可取。

笨小孩转念一想，之前的随机转换活动等策略不是会产生一个固定的挨揍概率吗？并且只要妈妈回来的时间不是特别早，这个概率就是可靠的。挨揍概率只与活动转换概率有关，所以只要选择合适的活动转换概率，就可以得到想要的挨揍概率。

笨小孩明确了想要的挨揍风险，也就有了目标平稳分布。根据平稳分布的性质，活动转换的概率需要满足

$$\pi(X)=\sum_{X'\in \{t,h\}} \pi(X')P(X\vert X')$$

一个平稳分布不足以确定一个转移矩阵，可以对矩阵加入一些限制。例如细致平衡条件（detailed balance condition）：

$$\pi(X)P(X'\vert X)=\pi(X')P(X\vert X')$$

细致平衡条件是平稳分布的充分不必要条件。满足细致平衡条件一定满足平稳分布的条件，因为

$$\sum_{X'}\pi(X')P(X\vert X')=\sum_{X'}\pi(X)P(X'\vert X)=P(X),\\ \int \pi(x')p(x', x)dx' = \int \pi(x)p(x, x')dx' = p(x)$$

设笨小孩希望将挨揍的风险控制为$0.2$，则满足细致平衡条件要求

$$0.2 T_{th} = 0.8 T_{ht}$$

只需要$T_{th}=4T_{ht}$即可，例如$T_{th}=1, T_{ht}=0.25$，

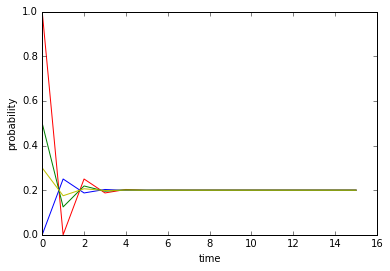
或者$P_{th}=0.5, P_{ht}=0.125$,

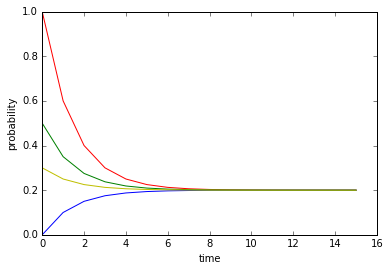
从两张图中可看出，两种活动转换概率下挨揍的概率最终都收敛于$0.2$，不同的是收敛速度。第一设定下变换活动的概率要大于第二种设定，因此第一种设定下可以在短时间内经历更多次转换，所以可以更快的收敛。不管怎样，笨小孩终于掌握了控制挨揍风险的方法。

这一过程涉及了三种概率分布：初始状态分布$P(X_0)$，状态转移分布$P(X_{i+1}\vert X_i)$和平稳分布$\pi(X)$。笨小孩做了一件非常了不起的事情，他通过设计状态转移分布得到了想要的平稳分布。

这其中的意义是非常远大的。这种设计状态转移分布来得到平稳分布样本的方法称为马尔可夫链蒙特卡洛(MCMC)，它可以说是占据了统计推断的半壁江山。

如果我们需要许多服从概率$p$的样本，而$p$又难以直接采样得出，我们可以采用笨小孩的方法，即构建一个转移分布$t$易于采样并且平稳分布为$p$的马尔可夫过程，在经过足够次采样后就可以得到服从$p$的样本。

具体来说，需要从$p(x)$中采样较困难，可以选择一个简单易于采样的建议分布$q(x\vert x’)$进行采样，然后根据某种概率$A(x’, x)$决定是否转移到刚采集的状态，使细致平衡条件得到满足：

$$p(x)q(x, x')A(x, x')=p(x')q(x', x)A(x', x)$$

这里，两边的状态转移概率分别为$t(x, x’)=q(x, x’)A(x, x’)$和$t(x’, x)=q(x’, x)A(x’, x)$。

根据从笨小问题中得到启示，为了使平稳分布更快收敛，需要尽可能使状态转换的概率大些。q(x’, x)的选择受可采样性限制，因此只能使$A(x’, x)$尽可能大。$A(x’, x)$作为概率，最大值为$1$。

假设$p(x)q(x, x’)>p(x’)q(x’, x)$，则$A(x, x’) < A(x’, x)$，令$A(x’,x)$取得最大值$1$，可求得$A(x, x’)=\frac{p(x’)q(x’, x)}{p(x)q(x, x’)}$;相反，如果$p(x)q(x, x’)<p(x’)q(x’, x)$，则$A(x, x’) > A(x’, x)$，令$A(x,x’)$取得最大值$1$，可求得$A(x’, x)=\frac{p(x)q(x, x’)}{p(x’)q(x’, x)}$，综合两种情况，可以统一写成

$$A(x, x')=\min(1, \frac{p(x')q(x', x)}{p(x)q(x, x')}).$$

此种采样算法称为Metropolis–Hastings算法。

Metropolis–Hastings算法

1. 随机设置$x_0$，令$\tau=0$;
2. 根据$q(x_{\tau}, x)$采出样本$x’$;
3. 从$[0, 1)$上得均匀分布随机采样$u$;
4. 如果$u<A(x_{\tau}, x’)$,令$x_{\tau+1}=x’$,否则令$x_{\tau+1}=x_{\tau}$;
5. 令$\tau = \tau + 1$;
6. 跳至第2步；

Metropolis-Hastings算法可以得到一系列样本$x_0, x_1, \cdots$。尽管相邻的样本之间不是互相独立的，但是可以每隔$M$间隔取一个样本，只要$M$足够大，就可以得到相互独立且分布为$p(x)$的随机样本。

在$A(x, x’)$中，$p$和$q$都同时出现在分子和分母中，因此没有必要明确地求出$p$和$q$的值后带入计算。因为在实际问题中，明确求$p$和$q$的值常涉及到求和或者积分，例如

$$p(x) = \frac{f(x, z)}{\int f(x, z') dz'}$$

或者

$$p(x)=\frac{f(x,z)}{\sum_{z'} f(x, z')}$$

计算分母的开销可能非常大甚至根本无法计算出来。由于分母在$A(x, x’)$的公式中可以被消去，因此可以直接使用未归一化的$f(x, z)$代入求解，大大地减少计算量。

Metropolis算法和Gibbs采样

Metropolis-Hastings算法中使用不同类型的建议分布$q$可以得到更具体的算法。

Metropolis算法是Metropolis-Hastings算法的特例。在该算法中，$q$选择对称的分布

$$q(x, x')=q(x', x)$$

接收率$A(x, x’)$即可表示为

$$A(x, x')=\min(1, \frac{p(x')}{p(x)}).$$

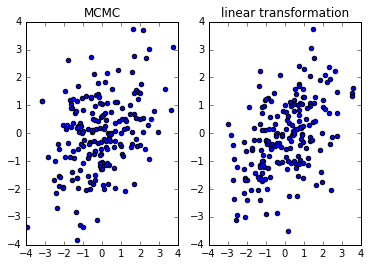
举个例子，假装我们不知道多元高斯分布如何直接采样，我们可以通过马尔可夫链蒙特卡洛方法来得到样本。由于多元标准高斯分布容易采样，我们可以令$q$为一个多元标准高斯分布，即

$$q(x, x') = \mathcal{N}(x'\vert x, I)，$$

应用Metropolis算法。下图展示采用Metropolis算法和线性变换算法得到多元非标准高斯分布的样本。可以看出，两种方法得到样本类似。

Metropolis-Hastings算法的令外一种著名的特例为Gibbs采样。该算法主要用来解决高维度状态空间的采样问题。

假设状态$x={x_1, x_2, \cdots, x_D}$包含$D$个维度，应用其它采样算法可能会导致接收率太低而使算法的效率降低。Gibbs采样的思路是相邻两个状态至多只有一个维度不同，并令

$$q(x, x')=P(x_i\vert x_{-i})$$

其中$x_{-i}$表示除了第$i$维以外的其它维度的数据。在这种情况下，

$$A(x, x')=\min(1, \frac{p(x')P(x_i\vert x'_{-i})}{p(x)P(x'_i\vert x_{-i})})\\ =\min(1, \frac{p(x_{-i})p(x_i'\vert x_{-i})p(x_i\vert x_{-i})}{p(x_{-i})p(x_i\vert x_{-i})p(x'_i\vert x_{-i})})=1.$$

Gibbs采样的接收率为$1$。在每一轮采样时，都要选取状态的某一维进行采样，既可以按顺序选取，也可以随机选取，但要保证各个维度均匀更新。

MCMC的问题

MCMC把大量原本不能计算的问题变得可以计算，具有非凡的意义。但是，MCMC往往只是把“不能”变为“能”，而无法进一步由“能”到“快”。

蒙特卡洛方法需要大量的独立同分布的样本，而马尔可夫链需要很长时间才能收敛，这两方面同时作用，使得MCMC非常低效，甚至无法在合理时间内解决某些应用。另外，马尔可夫链经历多久才能收敛到平稳分布没有很好的办法得知，不像其它方法有明确的指标（如神经网络的loss、变分推断的ELBO）指示模型是否已经收敛，使使用者不知什么时候该停止采样。

尽管如此，MCMC简单通用，常作为新模型的第一个推断算法，在实际和研究中应用仍然及其广泛。